X-orders and X-fixes in Expression Tree Traversal

X can be 'in', 'pre', or 'post'. They are used in similar context, but they refer to different things. What are the differences?

  • #compsci
  • #theory
  • Posted on 19 January 2023
  • 0.0 min read

Table of Contents

  1. X-order
  2. X-fix
    1. Simple Example
    2. Complex Example

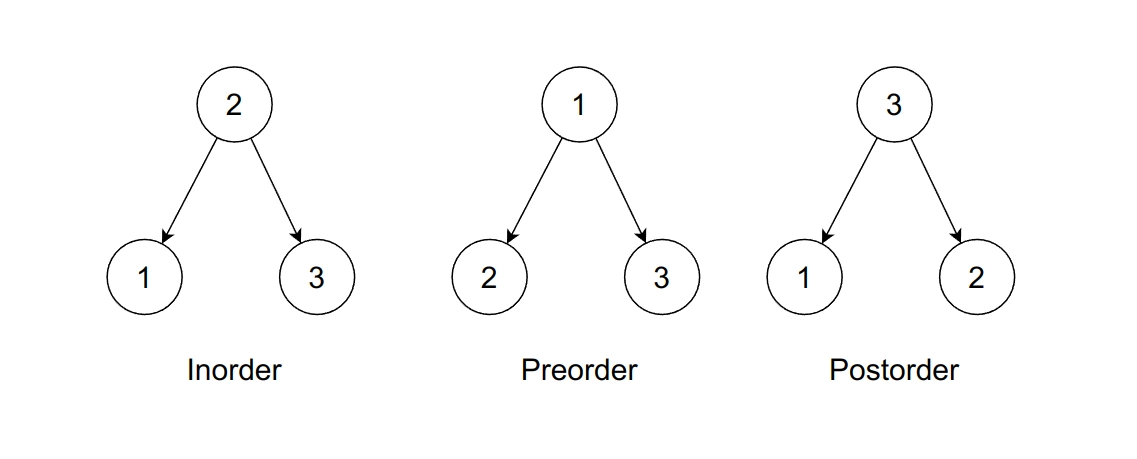
X-order

X-orders are typically used to describe the specific order in which the nodes are visited in a tree traversal algorithm.

  • Inorder traversal: visits the left subtree, root, and right subtree.
  • Preorder traversal: visits the root, left subtree, and right subtree.
  • Postorder traversal: visits the left subtree, right subtree, and root.

Each traversal algorithm has its own use cases, and the choice of algorithm depends on the specific problem being solved.

For example, inorder traversal is often used to visit all the nodes of a binary search tree in ascending order, while postorder traversal is used to delete all nodes of a binary tree.

Difference between inorder, preorder, and postorder
Difference between inorder, preorder, and postorder

X-fix

X-fix, also called x-fix notation is a way of writing mathematical expressions.

  • Infix notation is the standard notation used in most programming languages, and it is the notation that people are most familiar with. In infix notation, the operator is placed between the operands.
  • Prefix notation, also called Polish notation, is a way of writing mathematical expressions in which the operator comes before the operands.
  • Postfix notation, also called reverse Polish notation, is a way of writing mathematical expressions in which the operator comes after the operands.

In summary, each of these notation has its own characteristics and use cases. The differences between the three notations are the position of the operator in relation to the operands.

Simple Example

Take a look at the following expression tree:

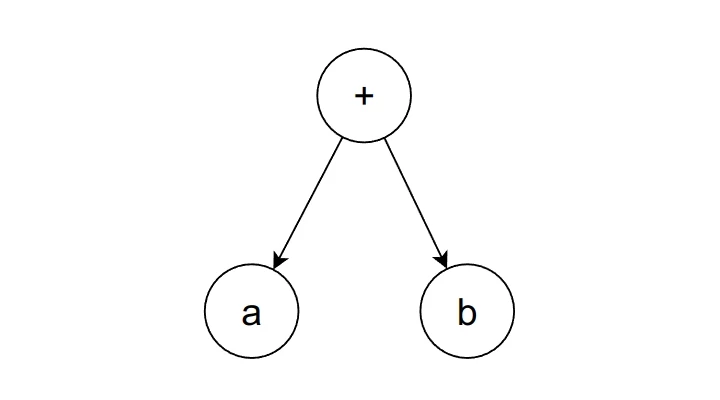
Expression tree example
Expression tree example

This tree could be represented in every fixes, pay attention to the position of the operator:

  • Infix notation: a+ba + b
  • Prefix notation: + a b+\ a\ b
  • Postfix notation: a b +a\ b\ +

Complex Example

The expression below comes from the last post:

(x2y−xz)+{(2yzx+y)/(x+y2)}\left( \frac{x^{2}}{y-xz} \right)+\left\{ \left( 2\frac{yz}{x+y} \right) / \left( x+y^{2} \right) \right\}

And we’ve made the expression tree for it:

Expression tree example 2
Expression tree example 2

If we try to form the infix notation, we’ll get

x∧2/y−x∗z+2∗y∗z/x+y/x+y∧2x\land2/y-x*z+2*y*z/x+y/x+y\land2

That’s why in infix notation we have to use brackets to indicate the order of operations and to group together sub-expressions that should be evaluated as one. This ensure that the expressions are evaluated in the intended order and make it more readable.

  • Infix notation
(x∧2/y−x∗z)+((2∗(y∗z)/(x+y)/x+y∧2)(x\land2/y-x*z)+((2*(y*z)/(x+y)/x+y\land2)
  • Prefix notation
+ / ∧ x 2 − y ∗ x z / ∗ 2 / ∗ y z + x y + x ∧ y 2+\ /\ \land\ x\ 2\ -\ y\ *\ x\ z\ /\ *\ 2\ /\ *\ y\ z\ +\ x\ y\ +\ x\ \land\ y\ 2
  • Postfix notation
x 2 ∧ y x z ∗ − / 2 y z ∗ x y + / ∗ x y z ∧ + / +x\ 2\ \land\ y\ x\ z\ *\ -\ /\ 2\ y\ z\ *\ x\ y\ +\ /\ *\ x\ y\ z\ \land\ +\ /\ +

While the prefix and postfix looked like they’re the inverse of each other, they actually have different orders. Be careful not to easily get trapped on this slight similarity.

Loading comments...