Constructing an Expression Tree

Constructing an Expression Tree thumbnail image

The step-by-step process of constructing an expression tree to evaluate mathematical expressions

  • #compsci
  • #theory
  • Posted on 15 January 2023
  • Last Updated on 19 January 2023
  • 0.0 min read

Table of Contents

  1. Definition
  2. Structure
  3. Construction

Definition

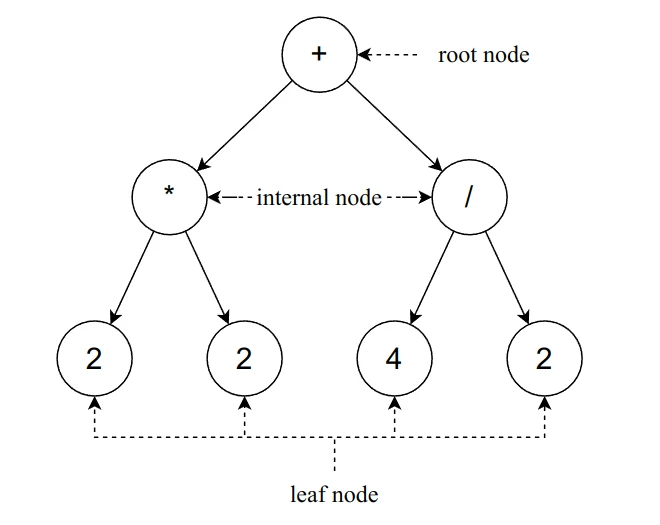
Expression tree is a binary tree data structure that can be used to represent mathematical expressions. An expression tree has the following properties:

  • Each leaf node is an operand. Example: 1, 72, a, x, y
  • The root node and internal nodes are operators. Example: +, -, *, /, ^
  • The tree is organized in a way that reflects the order of operations
  • The tree can be traversed in various techniques such as inorder, preorder, and postorder traversal

Structure

(2∗2)+(4/2)(2*2)+(4/2)

The expression tree consists of nodes, there must always be a root node to connect the expression together. A node that doesn’t connect with another node is called as leaf node, if it connects with another node then it’s called as internal node or just a node for short.

A basic structure of the expression tree
A basic structure of the expression tree

Construction

The construction of an expression tree can be done in various ways, usually using the stack data structure. In this post, we’ll do it without the help of stack.

We’ll have to know operator precedence:

  1. Parentheses ((…))
  2. Exponent (^)
  3. Multiplication and divison (*, /)
  4. Addition and substraction (+, -)

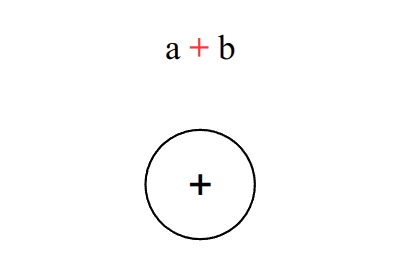
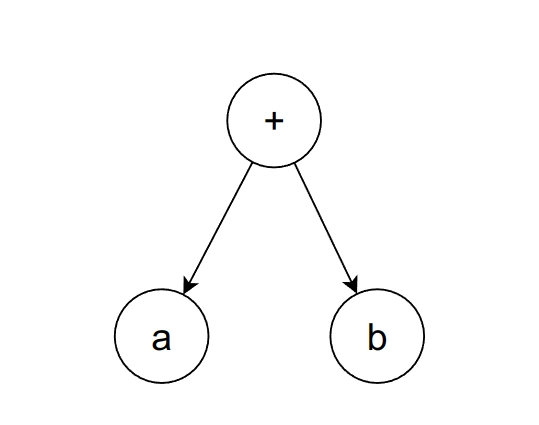
To begin with, let’s start with a simple expression a+ba+b.

  1. First, find the operator. In this example, it’s an addition (+)
Create a node with the operator
Create a node with the operator
  1. Find both of the operands and make sure the placement is correct. In this example, aa for the left leaf and bb for the right leaf
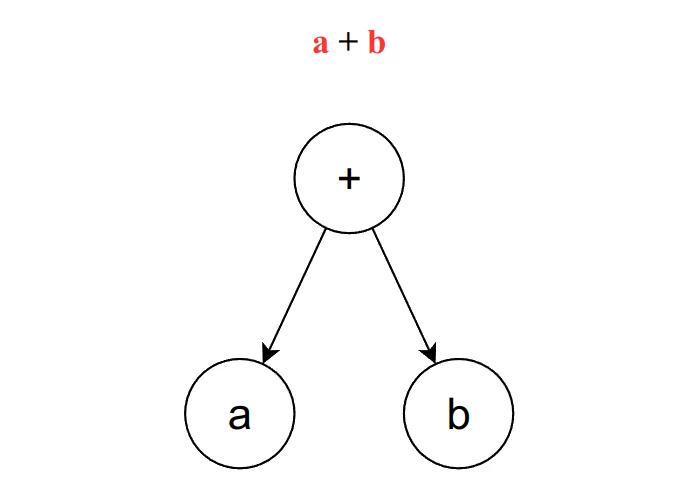
Create each leaf nodes with the operand
Create each leaf nodes with the operand

In just 2 steps, we have successfully made an expression tree.

What if there are a lot of operations?

Consider the following expression:

(x2y−xz)+{(2yzx+y)/(x+y2)}\left( \frac{x^{2}}{y-xz} \right)+\left\{ \left( 2\frac{yz}{x+y} \right) / \left( x+y^{2} \right) \right\}

It sure looks very complicated, but we can do this slowly and carefully by separating each operation and assuming “deeper” operations as a variable.

Assuming the following:

a=x2y−xzb=(2yzx+y)/(x+y2)\begin{align} a&=\frac{x^{2}}{y-xz} \notag \\[1em] b&=\left( 2\frac{yz}{x+y} \right) / \left( x+y^{2} \right) \notag \\ \end{align}

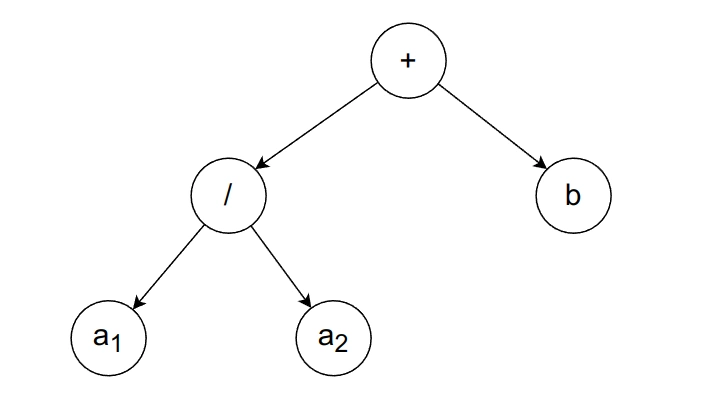
Start with getting the first operation for the root node.

a+ba+b
Yet another a + b expression tree
Yet another a + b expression tree

Right after getting the root node, we could start working from left-to-right. Let’s break this down:

a=x2y−xza1=x2a2=y−xz\begin{align} a&=\frac{x^{2}}{y-xz} \notag \\[0.75em] a_1&=x^{2} \notag \\ a_2&=y-xz \notag \end{align}
Adding leaf nodes to the "a" node
Adding leaf nodes to the "a" node
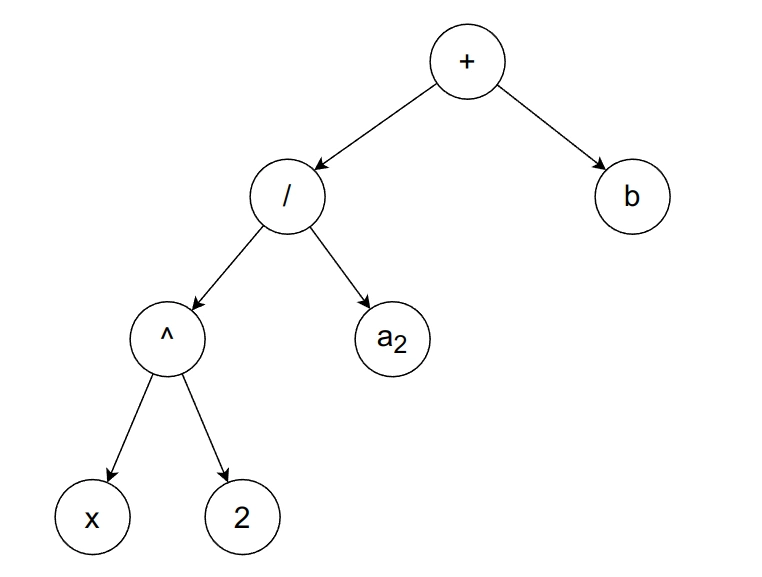
Substitute x ^ 2 to a1, don't forget to change the operator node
Substitute x ^ 2 to a1, don't forget to change the operator node

a2=y−xza_2=y-xz is a substraction of yy and x∗zx * z.

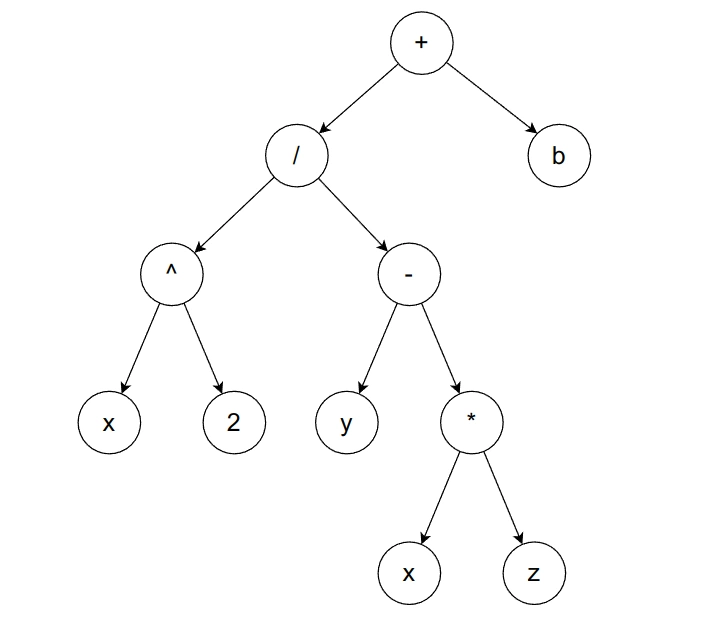
Add the other nodes
Add the other nodes

At this point, the process has gotten repetitive. In short, you have to repeat this way until every operation has been included in the tree.

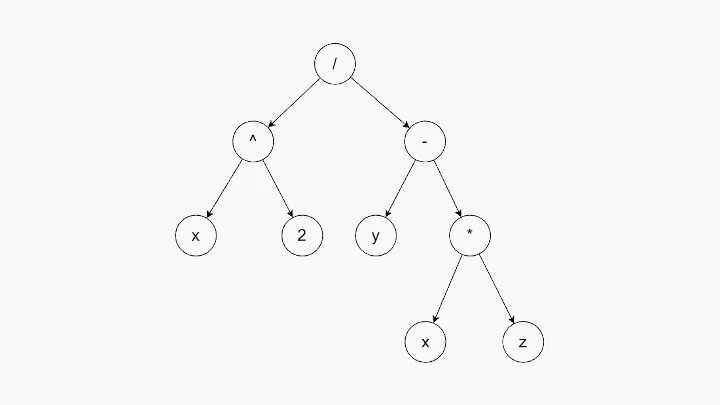
Try to construct the expression tree for bb by yourself, you may compare yours with the completed tree below:

Finalized expression tree
Finalized expression tree

Are there any other methods?

Yes, just like mentioned earlier, using stack data structure is one of the most common way to make expression trees. Another method is to construct your tree from the bottom by finding the deepest operations first. While there is no right or wrong with any method, you may want to try the others and see which one’s easier.

Loading comments...